https://www.acmicpc.net/problem/1654
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static int k;
public static int n;
public static int result;
public static long[] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
k = sc.nextInt();
n = sc.nextInt();
arr = new long[n];
result = 0;
for (int i = 0; i < k; i++) {
arr[i] = sc.nextInt();
}
Arrays.sort(arr);
long start = 1; // 시작이 arr[0]이 아니라 1임!
long end = arr[n - 1];
long mid;
long total;
while (start <= end) {
total = 0;
mid = (start + end) / 2;
for (int i = 0; i < n; i++) {
if (arr[i] >= mid) {
total += (arr[i] / mid);
}
}
// 랜선의 길이가 충분한 경우 total이 n에 맞춰질 수 있도록 짧게 잘라주기
if (total >= n) {
start = mid + 1;
}
// 랜선의 길이가 부족한 경우 더 많이 자르기
else if (total < n) {
end = mid - 1;
}
}
System.out.println(end);
}
}
|
cs |
문제를 풀어감에 있어서 중요한 요소
1. 이진탐색으로 풀자.
선형탐색으로 할 경우 주어진 랜선의 길이와 잘라낼 랜선의 길이의 값의 범위가 매우 크기때문에 시간초과에 걸릴 수 있다. 그러니 값의 범위를 효율적으로 줄여줄 수 있는 이진탐색을 이용해야한다!
2. 자료형을 long을 이용해야한다!
앞서 말했듯이 값의 범위가 엄청 크다. 그래서 int쓰면 안된다.
3. 이진탐색의 시작값은 arr[0]이 아니라 1
처음 생각할 때는 입력받아준 수들을 arr배열에 넣어서 정렬을 시킨후 얘네들 끼리의 이진탐색을 해야하는줄 알았다.
근데 생각해보니 가장 작은 값이 457이고 가장 큰값이 802인데 얘네를 최대로 이진탐색하면 start=457 end=458 밖에 안된다. 어떻게 200이 나올 수 있을까.. 를 생각해보면 그냥 시작을 1로 해주면 해결될 문제였다. 그렇게 하면 이진탐색을 했을 때도 end값이 200이 나올 수 있으며 랜선을 최대한 많이 잘라낼 수 있다. (start를 1로 잡아도 랜선을 잘라내는덴 아무런 영향을 미치지 않는다. 이진탐색을 통해 나온 mid값은 랜선의 개수를 생각하는데만 쓰이기 때문에 )
그리고 초기값을 0으로 선언해줘도 되지 않을까? 싶을 수도 있는데 문제에서 랜선의 길이는 자연수로 명시해줬고
total += (arr[i] / mid);
만약 초기값이 0이라면 0으로 나누는 일이 생길 수도 있는데 분모에는 0이 오지 못한다.
참고자료
https://st-lab.tistory.com/269
[백준] 1654번 : 랜선 자르기 - JAVA [자바]
https://www.acmicpc.net/problem/1654 1654번: 랜선 자르기 첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000..
st-lab.tistory.com
문제를 풀면서 궁금했던 것
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
if (total == n) { //왜 안되는 것일까?
System.out.println(end);
break;
}
// 랜선의 길이가 충분한 경우 total이 n에 맞춰질 수 있도록 짧게 잘라주기
else if (total > n) {
start = mid + 1;
}
// 랜선의 길이가 부족한 경우 더 많이 자르기
else if (total < n) {
end = mid - 1;
}
|
cs |
궁금한게 생겼는데, total==n일때 break를 걸어주면 안될까? 하는 의문이다. 즉, 랜선의 길이가 11이 될때 바로 break를 걸어주고 출력해보려는 생각이 들었다. 그랬더니 400이 나왔다. 시작값이 0, 끝값이 400, 중간값이 200이 될때
2+2+3+4=11로 랜선의 길이는 11이 잘 나오는데 왜 끝값이 200이 아니라 400이 나왔을까?
우선 최대 길이를 출력하는 것이기 때문에 end를 출력하는 것이 맞다.
그러면 처음부터 진행과정을 생각해보자.
처음에 start=1 end=802 mid=401일 것이다.
401로 원소들을 나누면 랜선의 길이는 5가 되기 때문에 end=400으로 맞춰준다.
start=1 end=400 mid=200이 된다.
200으로 원소들을 나누면 2+2+3+4=11이 된다. 우선 이 값을 저장하고
start<=end가 될때까지 돌려볼거다. 왜냐면 이 문제는 문제 풀이 초반에서 우리가 원하는 값이 나왔지만 우선 저장해둔다.
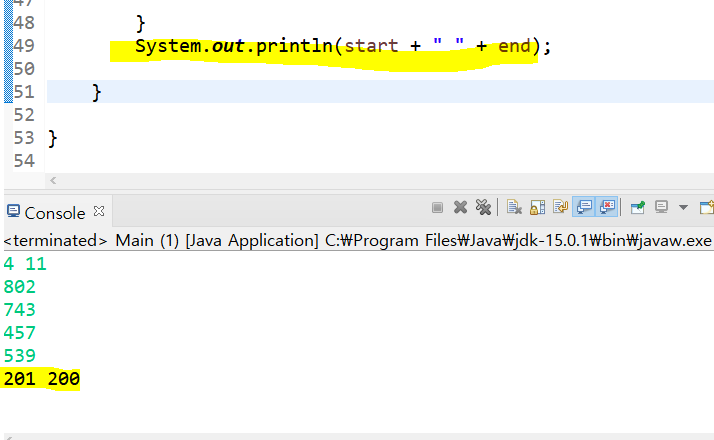
그리고 while문을 빠져나오기 전의 마지막 start값은 201 end=202 mid=201인데
2+2+3+3=10이여서 end-1 즉, end에는 200이 저장되면서 빠져나오게 된다.
이렇게 start>end 가 될때까지 탐색해야 탐색이 완료된다.
https://wootool.tistory.com/62
[알고리즘] 이분 탐색
이분 탐색 탐색 기법중에 하나로 원하는 탐색범위를 두 부분으로 분할해서 찾는 방식입니다. 그렇기에 원래의 전부를 탐색하는 탐색 속도에 비해 빠릅니다. 이분 탐색을 하는 방법은 left , right
wootool.tistory.com
이 글의 움짤을 보면 더 잘 이해될 것이다.
자 그러면 우리가 원하는건 최대 랜선 길이이고 이건 end를 뜻한다. 즉, 랜선들을 end로 나눴을 때 그 길이의 합이 11이 되는 것중에 가장 큰 end를 찾아내는 것이다.
start =1 end =400 mid =200 의 경우 end인 400으로 랜선을 나누면 1+1+1+2=5가 되므로 얘는 길이가 11이 아니기에 만족하지 않는다. 즉, 내가 놓친부분은 200이 mid가 아니라 end일때를 생각해주지 않았다.
답은 while문을 빠져나왔을 때의 end값 200이다.
추가로 덧붙이자면 이 문제는 upper bound형식을 활용해야 한다.
그렇기 때문에 total<n에 등호를 붙여주면 안되는거다. 왜냐면 198,199,200으로 자를때 모두11인데
이들 중 최대 길이를 찾기 위해서는 upperbound를 해줘야한다.
랜선의 개수가 11보다 작으면 최대 길이를 1만큼 줄이고, 11보다 크면 최소 길이를 1만큼 늘려서 자르고자 하는 길이를 늘린다.
'알고리즘 > 이진탐색' 카테고리의 다른 글
| [java 백준] 골드 5/ 2110번 공유기 설치 (0) | 2022.01.26 |
|---|---|
| [java 백준] 실버 4/10816번 숫자카드 2 (0) | 2022.01.26 |
| [java 백준] 실버 4/10815번 숫자카드 (0) | 2022.01.24 |
| 이진탐색 알고리즘 (0) | 2022.01.22 |
| [java 백준] 실버 3/ 2805번 나무자르기 (0) | 2022.01.22 |


댓글