https://www.acmicpc.net/problem/1783
1783번: 병든 나이트
첫째 줄에 체스판의 세로 길이 N와 가로 길이 M이 주어진다. N과 M은 2,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static int n;
public static int m;
public static int cnt;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
if (n == 1) {
cnt = 1;
} else if (n == 2) {
// 4가 최대
cnt += Math.min(4, (m + 1) / 2);
} else if (n >= 3) {
if (m < 7) {
cnt += Math.min(4, m);
} else {
cnt += 5 + (m - 7);
}
}
System.out.println(cnt);
}
}
|
cs |
이 문제는 세로를 기준으로 풀어주는 것이 좋은 것 같다. 난 처음에 가로가 7이 될때(이때가 1번부터 4번 나이트를 모두 쓴 경우)를 기준으로 나눠서 풀어주려했는데 이러면 생각해 줄 것 이 너무 많았다.
범위를 타이트하게 좁혀서 세로가 1일때, 2일 때, 3 이상일 때 로 나누고 3 이상일 때 가로를 7을 기준으로 나눠주는 것이 현명한 방법이였다.
우선 세로가 1일때를 보자.
1일때는 처음 시작하는 곳만 방문하기에 cnt는 1이다.
세로가 2일때
가로가 3까지 있다면
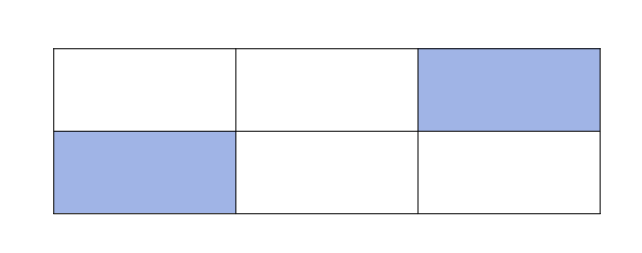
2곳 방문 가능
가로가 5까지라면

3곳 방문이 가능하다.
이걸 식으로 나타내면 cnt+=(n+1)/2;로 써줄 수 있다.
단 얘도

가로가 7일 때까지만 가능하고, 가로가 7보다 더 길어지면 cnt가 5보다 크거나 같아지기 때문에 4개의 나이트를 써야한다. 하지만 세로가 2일때 4개의 나이트를 모두 쓸 수 없기에 세로가 2일때의 최대방문 값은 4가 된다.
그래서 이걸 코드로 나타내면 Math.min(4,(n+1)/2);
세로가 3이상일때를 생각해보자.
왜 3이 기준이냐 한다면 세로가 3일 때부터 나이트 4개를 모두 사용할 수 있기 때문이다.
세로가 3이고, 가로가 4일때 까지를 보자.

가로가 1이면 cnt=1
가로가 2이면 cnt=2
가로가 3이면 cnt=3
가로가 4이면 cnt=4이다
그럼 여기서 생각해볼 수 있는 것은 어쨌든 최대값이 4라는것이고, 가로길이가 4이하까지는 cnt+=m;이라고 코드를 쓸 수 있겠다.
그러면 나이트를 모두 사용해줄 수 있는 범위인 가로 7이상 전까지
가로 5와 가로 6의 경우는 어떻게 될까?
여기서 부터는 5개 이상으로 쓰게 될 수 있기에 나이트 4개를 쓰도록 해야한다.
가로가 5일때


이렇게 경우의 수가 2개 있는데 어쨌든 최대는 4이다. 가로가 6일때도 최대가 4인것을 알 수 있다.
그래서 가로 7미만까지 cnt+=Math.min(4,m); 이라 할 수 있겠다.
가로가 7이상인 경우를 보자.
가로가 7일때는 당연히 5이다.

이렇게 나이트 4개를 모두 써줘야한다.
가로가 10일때를 한번 보자.

7일때 까지 5개 더해주고, 8부터는 방문횟수가 가로가 1늘어날때 마다 횟수도 1늘어난다.
이는 2칸 위로,1칸 오른쪽/ 2칸 아래로,1칸 오른쪽 조합이 가장 최대로 방문할 수 있는 조합이기 때문이다.
그러면 이걸 식으로 나타내보면
cnt+=5+(m-7);이 되겠다.
문제를 풀며 아쉬웠던 점 + 반성
그리디는 규칙을 찾기 위해 생각을 많이 해야하는데 지금 내가 생각을 잘 안하려하는것이 문제인 것 같다.
그리고 규칙에는 항상 기준이 있는데 기준을 잘 못세운것도 문제인것 같다. 이 문제는 세로를 기준으로,
나이트를 모두 움직일 수 있는 경우는 세로가 3, 가로가 7이상일때만 잘 인지했어도 어느정도 조건분기를 했을 것 같다.
앞으로 남은 그리디 문제들은 1시간 말고 2시간 정도로 생각하는 시간을 늘려야겠다. 다음에 푸는 문제는 꼭 규칙을 잘 찾아내 보자.
참고사이트
https://songwonseok.github.io/algorithm/BOJ-1783/
백준 1783: 병든 나이트(Java)
문제링크 : https://www.acmicpc.net/problem/1783
songwonseok.github.io
'알고리즘 > 그리디' 카테고리의 다른 글
| [java 백준]골드 4/ 1744번 수묶기 (0) | 2022.02.11 |
|---|---|
| [java 백준] 실버 2/1931번 회의실 배정 (0) | 2022.02.08 |
| [java 백준] 실버 5/ 10610번 30 (0) | 2021.11.04 |
| [java 백준]브론즈 3/ 2875번 대회 or 인턴 (0) | 2021.09.19 |
| [java 백준] 실버2/11047번 동전 0 (0) | 2021.08.10 |
댓글