피보나치 수열
f(n) = f(n-1) + f(n-2) (단, n>2)
이것을 자바 코드로 구현해 보면,
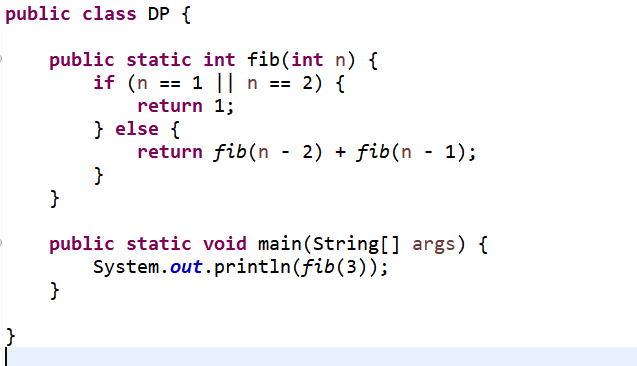
fib(3)이면 결과는 2일 것이다. f(1)=1이고,f(2)=1이기 때문에 f(3)은 2가 된다.
Memoization
피보나치 수열은 이미 계산한 수를 중복으로 계산하는 경우가 발생하기 때문에 굉장히 비효율적이다.
계산의 중복을 피하기 위해 이미 계산된 값을 기억해두는 것.
Memoization에서 저장해 놓은 배열을 cache 라고 부른다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public class DP {
static int[] f = new int[10000];
static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
} else if (f[n] > -1) {
return f[n];
} else {
f[n] = fib(n - 2) + fib(n - 1);
return f[n];
}
}
}
|
cs |
여기서는 f가 cache이다.
else if (f[n] > -1) {
return f[n];
}
--> 배열 f가 -1으로 초기화되어있다고 가정하는 것이다. 즉 이미 계산된 값이라는 의미이다.
else {
f[n] = fib(n - 2) + fib(n - 1);
return f[n];
}
--> 중간 계산 결과를 catching한다. 이로써 중복계산을 피하게 된다.
Bottom-up 방식
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public class DP {
static int[] f = new int[10];
static int fib(int n) {
f[1] = f[2] = 1;
for (int i = 3; i <= n; i++) {
f[n] = f[n - 1] + f[n - 2];
}
return f[n];
}
}
|
cs |
순차적으로 올라가는 방식으로 cache에 저장한다.
즉, 가장 작은 subproblem에서 부터 시작해서 원하는 값을 구해내는 것이다.
예를 들어 f(n)을 구하고 싶을 때, f(0),f(1),f(2)....f(n)까지 구해내는 방식이다.
이항계수
고등학교 때 확통을 많이 까먹어서 조합부터 다시 기억해보면

이항계수는

n C k=(n-1) C k+(n-1) C (k-1) (단,n>=k)
이 공식을 자세히 보면 확통 시간에 배웠던 이항정리 단원에서 파스칼의 삼각형과 비슷하다는 것을 알 수 있다!!
이 식을 자바코드로 바꿔보면
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public class DP {
int binomial(int n,int k) {
if(n==k||k==0) {
return 1;
}
else {
return binomial(n-1,k)+binomial(n-1,k-1);
}
}
}
|
cs |
예를 들어 5 C 3을 계산한다면

3 C 2가 2번이나 계산되므로 비효율적이다. 그러므로 이를 Memoization과 bottom - up 방식으로 풀어보겠다.
Memoization - 이항계수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
public class DP {
int [][] binom=new int[10][10];
int binomial(int n,int k) {
if(n==k||k==0) {
return 1;
}
else if(binom[n][k]>-1) { // 배열 binom이 -1로 초기화되었다고 가정
return binom[n][k];
}
else {
binom[n][k]=binomial(n-1,k)+binomial(n-1,k-1);
return binom[n][k];
}
}
}
|
cs |
bottom-up 방식 - 이항계수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public class DP {
static int[][] binom = new int[10][10];
static int binomial(int n, int k) {
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= i && j <= k; j++) {
if (k == 0 || n == k) {
binom[i][j] = 1;
} else {
binom[i][j] = binom[i - 1][j - 1] + binom[i - 1][j];
}
}
}
return binom[n][k];
}
}
|
cs |
정리
- 순환식을 계산하는 기법
- 둘 다 동적 계획법의 일종으로 보기도 한다.
- Memoization은 top-down 방식, 실제로 필요한 subproblem만을 푼다
- 동적 계획법은 bottom - up 방식이며, recursion에 수반되는 overhead가 없다
(overhead = 위키 백과에 따르면 '특정 작업을 수행하는 데 필요한 초과 또는 간접 계산시간 '을 말한다.)
'알고리즘 > DP' 카테고리의 다른 글
| [java 백준] 실버 3/ 11727번 2xn타일링 2 (0) | 2021.07.30 |
|---|---|
| [java 백준] 실버 3/ 11726번 2 x n 타일링 (0) | 2021.07.28 |
| [java 백준] 실버 3/ 9095번 1,2,3 더하기 (0) | 2021.07.28 |
| [DP 개념] #2_동적계획법(1) (0) | 2021.07.28 |
| [java 백준] 실버 3/ 1463번, 1로 만들기 (0) | 2021.07.27 |


댓글