728x90
반응형
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import java.util.Scanner;
public class Main {
public static int n;
public static int[] arr;
public static int[] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
arr = new int[n + 3];
dp = new int[n + 3];
for (int i = 1; i <= n; i++) {
arr[i] = sc.nextInt();
}
dp[1] = arr[1];
dp[2] = arr[2] + arr[1];
dp[3] = Math.max(arr[1] + arr[3], arr[2] + arr[3]);
for (int i = 4; i <= n; i++) {
dp[i] = Math.max(dp[i - 3] + arr[i - 1] + arr[i], dp[i - 2] + arr[i]);
}
System.out.println(dp[n]);
}
}
|
cs |
https://we1cometomeanings.tistory.com/85
[java 백준] 실버 1/ 2156번 포도주 시식
https://www.acmicpc.net/problem/2156 2156번: 포도주 시식 효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을
we1cometomeanings.tistory.com
2156번 포도주시식 문제랑 문제푸는 방식이 비슷했다!
근데 중요한 것은 마지막 계단은 꼭 밟아야 하는데 첫번째 계단은 굳이 안밟아도 된다!
dp[3] = Math.max(arr[1] + arr[3], arr[2] + arr[3]);
그래서 위와 같은 코드가 나오는 것이다. 첫번째 세번째를 밟는경우, 두번째 세번째를 밟는 경우 중 가장 큰 값을 고르면된다.
만일 n이 4이고 계단이 10 20 15 25 순으로 있을 때, 점화식을 세울 수 있는 방법은
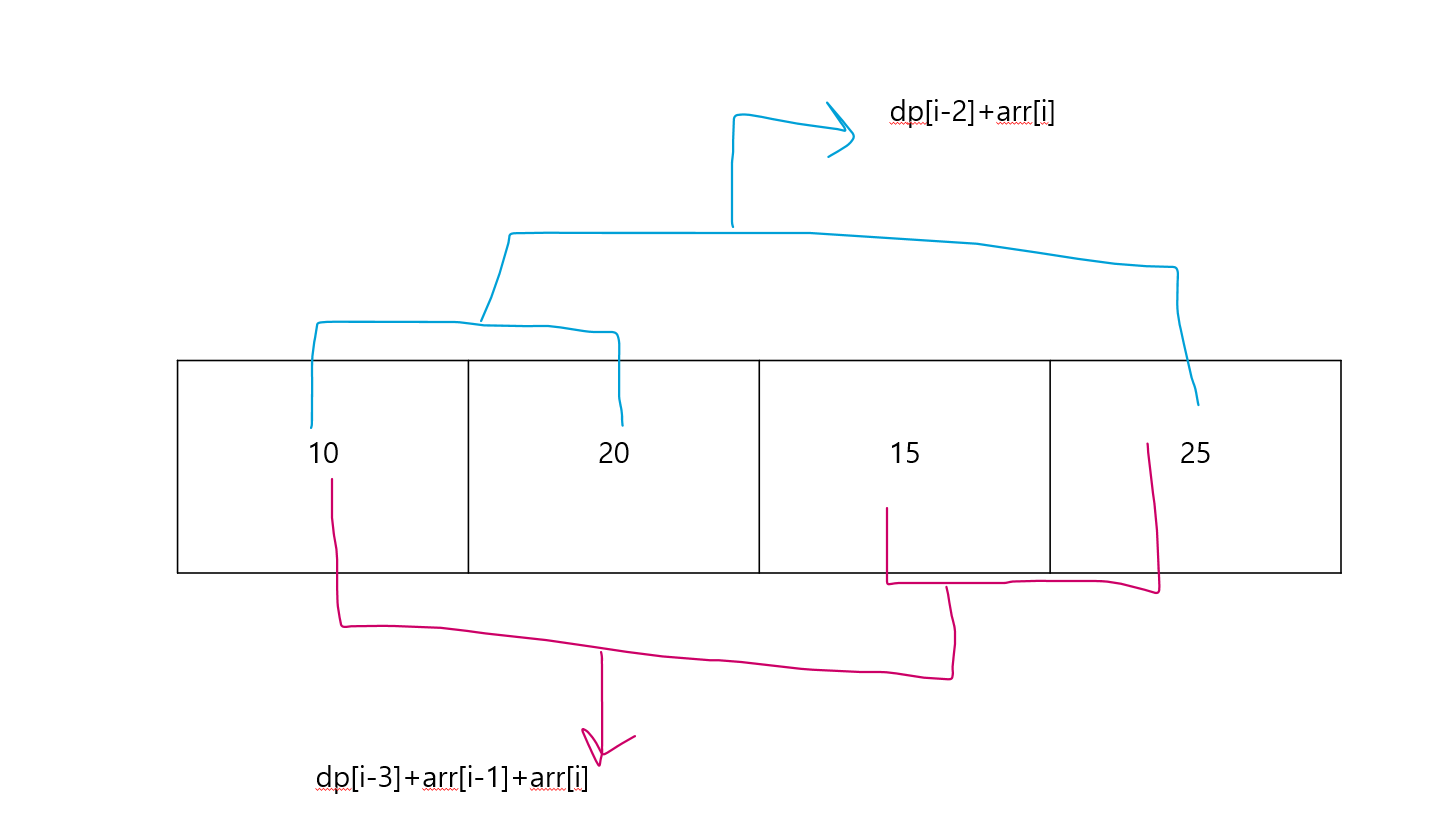
분홍, 파랑 중에서 더 큰 값을 택하면 된다.
여기서 첫번째 계단을 더해준 것은 반드시 넣어야 하는 것이 아닌 첫번째 계단을 더해줘야 계산한 값이 더 커지기 때문이다!
728x90
반응형
'알고리즘 > DP' 카테고리의 다른 글
| [java 백준] 실버 2/ 11055번 가장 큰 증가 부분 수열 (0) | 2021.08.05 |
|---|---|
| [java 백준] 실버 2/1912번 연속합 (0) | 2021.08.05 |
| [java 백준] 실버 2/11722번 가장 긴 감소하는 부분 수열 (0) | 2021.08.04 |
| [java 백준] 실버 2/11053번 가장 긴 증가하는 부분 수열 (0) | 2021.08.04 |
| [java 백준] 실버 1/ 2156번 포도주 시식 (0) | 2021.08.03 |
댓글